Today I was trying to find a complete implementation of a heap in google. Although I found a couple of implementations using an array, I never found a single one that where complete and uses a binary tree instead. So I decided to implement one.
Now, briefly explained, a heap is a data structure that can keep the priority of a set of values and that the value with the highest priority can be accessed in O(1) time.
This structure have other properties, for example, to insert and prioritize an element takes O(log n) , and the same takes to remove the element with the highest priority.
Now, a heap implemented with an array can meet this requirements until you reach the end of the array, in which case the operation will fail or it will need to move all the elements to a bigger array, passing from a complexity of O(log n) to O(n).
Depending on the way the Heap-Array is implemented one of two things can happened. You could end with an implementation that makes a lot of memory reallocation but waste little memory or an implementation that makes fewer memory reallocations but may waste a lot of memory in a worst case.
On the other hand, an implementation with a binary tree doesn’t waste memory, doesn’t do memory reallocation and always perform insertions in O(log n), at least as far as you make a good implementation. I hope that mine is one of those.
Now, the tricky thing with a heap using a tree is how to find the place to store the new element.
In an array implementation you just keep a variable storing the number of elements in the heap and then with some pointer arithmetic you can access the slot in which you need to store the next element.
In a binary tree you can not access the node you want like that but instead you need to traverse the tree to find the next available slot.
Now, since in a heap tree you need to satisfy the Complete Binary Tree condition CBT, you need to store the new values in a Breadth First way, this is, you can not insert a node in a certain level if the previous level is not completely filled.
You can see this video that explains very well this property in a heap tree.
This lead to the problem of how to find that very specific place in an efficient manner. Sadly my well beloved wikipedia explains that step as “Add the element to the bottom level of the heap.” A rather ambiguous explanation and certainly not very helpful.
The first thing we noticed is that we may be able to find the correct part in the tree with a slightly modified version of a BFS, the problem with that is that the complexity turns form O(log n) to O(n) and life became meaningless. The other solution becomes by analyzing how a binary search is performed.
Certainly you can not perform a binary search in something that is not sorted as for example, our binary heap but there is something interesting in this search that I’ll explain with some chars ![]() .
.
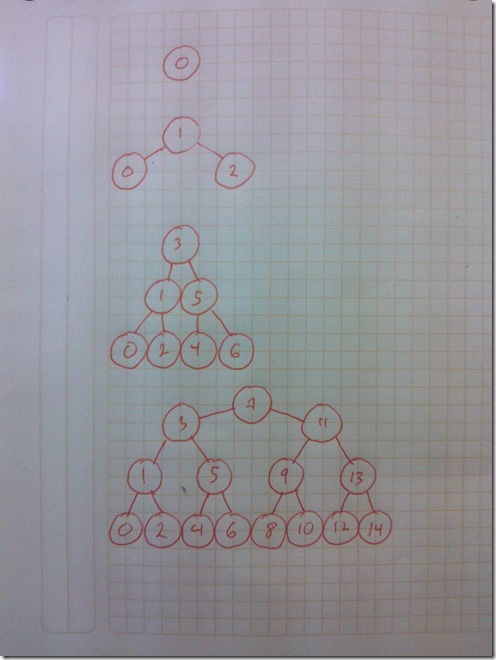
Up there you can see four balanced binary trees with only the numbers from 0 through the maximum capacity of the tree with a certain amount of levels. So for example in the first tree we only have 0 because that is all the elements that you can store in a one-level tree. In the four tree we have the elements from 0 to 14, that is 15 elements that is the maximum amount of elements you can store in a 4 level binary tree.
The number of elements that you can store in a n level tree is given by the formula 2n –1 .
Now If you haven’t realized, the last level in all the trees is filled with only even numbers, even more, all the even numbers in the tree are in that very last level. And of course that cero is an even number ![]() , just in case you where wondering.
, just in case you where wondering.
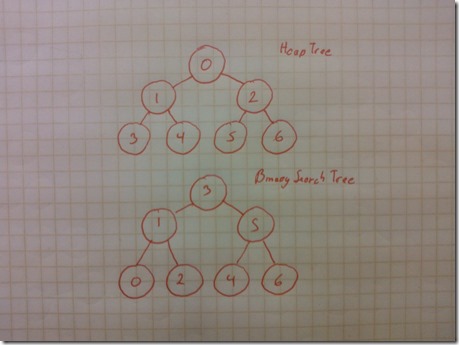
Now, that property is useful because of this next chart. Here you can see the way a heap is constructed and the way a balanced binary tree looks like.
As we discuses earlier, perform a binary search is easy and efficient, unlike performing a BFS that is slightly more complicated and not that efficient, so it would be nice to be able to perform a binary search instead of the BFS, the only thing we need is to transform the heap index to a binary search index and that is not too complicated.
So we have our desired heap index that for example could be that 3 in the heap-tree, and the index of where a binary search would perform efficiently, that is the 0 in the balanced binary tree.
We can realize that in the heap three the last level is filled with consecutive numbers, we can translate to start from zero if we simply subtract the number of elements that are in the higher levels, for the case of the last chart that number would be 3.
So our numbers would end like 0, 1, 2, 3 instead of 3, 4, 5, 6, now if we multiply each of these numbers times 2 we ended with a series of even numbers, that numbers are 0, 2, 4, 6 that is actually the numbers on the last level of the binary tree.
So we can came with the next magic formula.
(DesiredHeapTreeIndex – power(2, deepOfTree – 1) +1) * 2;
this part
power(2, deepOfTree – 1) +1
is the number of elements in the higher levels.
DesiredHeapTreeIndex this is the number we want to convert.
and the 2 is a 2 to convert it all to even numbers.
This will help us to make a binary search only because we are not looking for a specific value but instead for a specific position in the tree.
With this we can create a function that given a heap tree, its deep and the position return a pointer that points to that specific slot welter this is empty or not.
The function will look pretty much like that of a binary search.
Node ** getPonterofPosition(int dest, int current, int deep, Node ** root){ if(dest == current) return root; if(current > dest) getPonterofPosition(current - pow(2, deep-1), dest, deep-1, &(*root)->l); else getPonterofPosition(current - pow(2, deep-1), dest, deep-1, &(*root)->r); }
In the above function, the dest variable is the position we want to find, the current is the current node position, since we are not traversing a real balanced binary tree we need it to perform the binary search.
So a call to this function will look similar to this.
int htindex // the heap tree index Node * root;// the root of the tree int deep = (int)ceil(log((htindex+1)/log(2)); //calculating the deep of the tree. int dest = (htindex- pow(2, deep-1))*2; //converting from heaptree position into bt position int current = pow(2, deep-1)-1; Node ** lePointer = getPointerPosition(dest, current, deep-1, &root);
//Now we can increase htindex and store a new node in the obtained pointer.
htindex ++;
lePointer = new Node(2);
so there it is the node stored where it should be stored. Now wee need to implement all the other stuff for heapify the tree.
Now, because right now it is getting late, here are the whole implementation with the other shinny stuff ![]() , I promise to eventually finish this entry.
, I promise to eventually finish this entry.
#include <stdio.h> #include <stdlib.h> #include <stdbool.h> #include <math.h> #include <stdint.h> typedef struct Node{ struct Node * l; struct Node * r; int val; }Node; typedef struct Heap{ Node * root; bool isMaxHeap; int count; }Heap; Heap * createMaxHeap(){ Heap * h = (Heap*)calloc(1, sizeof(Heap)); if(h) h->isMaxHeap = true; return h; } Heap * createMinHeap(){ Heap * h = (Heap*)calloc(1, sizeof(Heap)); if(h) h->isMaxHeap = false; return h; } Node * createNode(int val){ Node * newNode = (Node *) calloc(1, sizeof(Node)); if(newNode) newNode->val = val; return newNode; } void insertAndHeapify(Node *n, Node **root, int current, int dest, int deep, bool isMaxHeap){ if(!(*root)){ *root = n; }else{ if( ( isMaxHeap && n->val > (*root)->val) || (!isMaxHeap && n->val < (*root)->val)){ n->val ^= (*root)->val; (*root)->val ^= n->val; n->val ^= (*root)->val; } if(current > dest) insertAndHeapify(n, &(*root)->l, current - (1<<(deep-1))/*current - pow(2, deep-1)*/, dest, deep-1, isMaxHeap); else insertAndHeapify(n, &(*root)->r, current + (1<<(deep-1))/*current - pow(2, deep-1)*/, dest, deep-1, isMaxHeap); } } bool insertInHeap(Heap* h, int val){ Node *n = createNode(val); if(!n) return false; h->count ++; int deep = (int)ceil(log(h->count+1)/log(2)); int dest = (h->count-(1<<(deep-1)))<<1; //= (h->count - pow(2, deep-1))*2; int current = (1<<deep-1)-1; //= pow(2, deep-1)-1; insertAndHeapify(n, &(h->root), current, dest, deep-1, h->isMaxHeap); } void Heapify(Node * root, bool isMaxHeap){ if(!root || (!root->l && !root->r)) return; Node * tmp; if(!root->l || !root->r) tmp = root->l ? root->l : root->r; else if (isMaxHeap) tmp = root->l->val > root->r->val ? root->l : root->r; else tmp = root->l->val < root->r->val ? root->l : root->r; if (isMaxHeap && (root->val >= tmp->val)) return; if (!isMaxHeap && (root->val <= tmp->val)) return; root->val ^= tmp ->val; tmp ->val ^= root->val; root->val ^= tmp ->val; Heapify(tmp, isMaxHeap); } Node * removeLastInsertion(Node **root, int current, int dest, int deep){ if(!(*root)) return NULL; if(current == dest){ Node *t = *root; *root = NULL; return t; }else if(current > dest) removeLastInsertion(&(*root)->l, current - (1<<(deep-1))/*current - pow(2, deep-1)*/, dest, deep-1); else removeLastInsertion(&(*root)->r, current + (1<<(deep-1))/*current - pow(2, deep-1)*/, dest, deep-1); } int peakFromHeap(Heap *h){ if(!h || !h->root) return 0; int deep = (int)ceil(log(h->count+1)/log(2)); int dest = (h->count-(1<<(deep-1)))<<1; //= (h->count - pow(2, deep-1))*2; int current = (1<<deep-1)-1; //= pow(2, deep-1)-1; int val = h->root->val; Node * t = removeLastInsertion(&(h->root), current, dest, deep-1); if(h->root) h->root->val = t->val; free(t); h->count --; Heapify(h->root, h->isMaxHeap); return val; } bool isHeapEmpty(Heap *h){ return h->root == NULL; } void printHeapInBFS(Heap * h){ if(!h || !h->root) return; Node ** q = (Node **) malloc(sizeof(Node*)*(h->count)); if(!q) return; int i = 0; int r = 0; q[i++] = h->root; while(i>r){ Node * tmp = q[r++]; printf("%i,", tmp->val); if(tmp->l) q[i++] = tmp->l; if(tmp->r) q[i++] = tmp->r; } printf("\n"); free(q); } void printInOrder(Node * root){ if( !root) return; printInOrder(root->l); printf("%i,", root->val); printInOrder(root->r); } void printHeapInOrder(Heap *h){ printInOrder(h->root); printf("\n"); } void printPreOrder(Node * root){ if( !root) return; printf("%i,", root->val); printPreOrder(root->l); printPreOrder(root->r); } void printHeapPreOrder(Heap *h){ printPreOrder(h->root); printf("\n"); } int main(void){ Heap * h = createMaxHeap(); //Heap * h = createMinHeap(); insertInHeap(h, 15); printHeapInBFS(h); insertInHeap(h, 14); printHeapInBFS(h); insertInHeap(h, 13); printHeapInBFS(h); insertInHeap(h, 12); printHeapInBFS(h); insertInHeap(h, 11); printHeapInBFS(h); insertInHeap(h, 10); printHeapInBFS(h); insertInHeap(h, 9); printHeapInBFS(h); insertInHeap(h, 8); printHeapInBFS(h); insertInHeap(h, 1); printHeapInBFS(h); insertInHeap(h, 2); printHeapInBFS(h); insertInHeap(h, 3); printHeapInBFS(h); insertInHeap(h, 4); printHeapInBFS(h); insertInHeap(h, 5); printHeapInBFS(h); insertInHeap(h, 6); printHeapInBFS(h); insertInHeap(h, 7); printHeapInBFS(h); printHeapInOrder(h); printHeapPreOrder(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); printf("peak: %i\n", peakFromHeap(h)); printHeapInBFS(h); }
cheers >.<